人工知能の発展は再び想像の境界を突破し、今回は数学証明が主役となりました。OpenAIの研究者たちが最近明らかにした衝撃的な発見によると、GPT-5Proは数学論文を読んだ後、オリジナルのより正確な数学的結論を導き出し、完全な証明プロセスを提示しました。このニュースは野火のように広がり、関連するツイートは半日以内に230万回以上の閲覧数を記録し、ネット上で熱烈な議論を巻き起こしました。
数学証明の歴史的な突破
出来事のきっかけは一見普通でした。OpenAIの研究者がGPT-5Proに凸最適化問題に関する学術論文を入力し、モデルの理解能力をテストしたかったのです。しかし、誰も予想していなかったのは、GPT-5Proが論文を丁寧に読み込んだ結果、一つの境界問題に対して原文よりも正確なしきい値を提示し、厳密な数学的証明プロセスを提供したことです。
この発見の意味は表面的な現象を越えています。これはAIが単なる人間の知識の繰り返しや整理者ではなく、本当に独立した思考と革新性のある推論能力を持っていることを示しています。GPT-5Proは既存の知識ベースから答えを探しているのではなく、数学的論理を使って独自の推論を行っているのです。このような能力の出現は、AI開発における重要な転機を示しています。
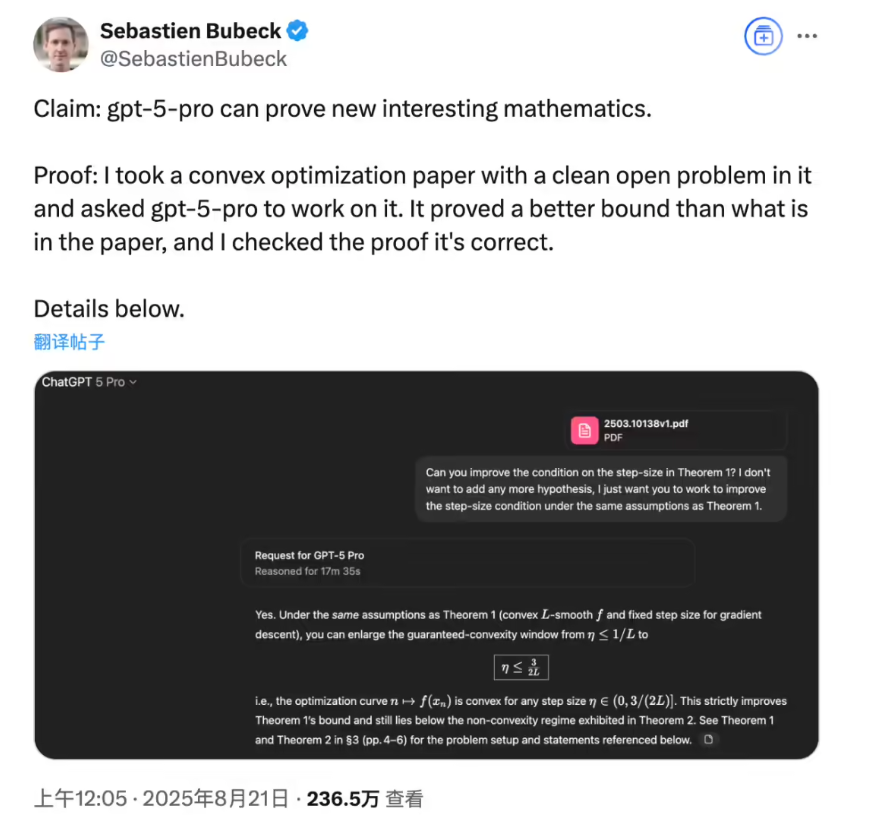
その研究結果を正式な論文として掲載しなかった理由は少しドラマティックでした。掲載準備中に元の論文著者が更新版を先に公開し、新しい境界結果を提示したのです。この新しい境界はGPT-5Proの発見をさらに超えており、人間の学者たちの迅速な反応は学術競争の激しさを示しています。
しかし、最も重要な発見はGPT-5Proの証明アプローチが人間の学者とは異なっていた点です。この差異はAIが単純な模倣や模倣ではないことを証明しており、真正の独立した探求と革新能力を持っていることを示しています。OpenAI社長のBrockman氏はこのように述べました。「生命の兆候」と表現し、AIが人間のような知能特徴を発展させている可能性を示唆しています。
凸最適化問題の数学的奥秘
GPT-5Proが挑戦した論文は、凸最適化分野の重要な問題について研究しています。凸最適化は、数学の最適化の重要な部分であり、凸集合内の凸関数の最小化問題を専門としています。機械学習、経済学、工学などの多くの分野で広く応用されています。

タイトルが「凸最適化曲線は凸ですか?」のこの論文では、勾配降下法を使って滑らかな凸関数を最適化する際に、生成される最適化曲線が凸性を持つのかという、一見簡単だが非常に重要な問題が取り上げられています。ここでの最適化曲線とは、関数値が反復回数とともに変化する曲線のことです。この曲線が凸であれば、最適化速度が単調に減少することを意味します。
論文の核心的な発見はステップサイズ(学習率)の選択の影響に焦点を当てています。研究によると、最適化曲線の凸性はステップサイズの設定に完全に依存しています。特定の範囲内でステップサイズを選べば、最適化曲線は凸性を保証できますが、あるしきい値を超えると、勾配降下法が収束しても最適化曲線が凸性を失う可能性があります。

GPT-5Proの魅力的なパフォーマンス
原論文の第一版では、著者はステップサイズが1/L以下および1.75/L以上の場合を成功裏に証明しましたが、その中間の区間については理論的空白がありました。まさにこの未探索領域で、GPT-5Proは非凡な数学的洞察力を発揮しました。
GPT-5Proはわずか17分半で、より細かい不等式のテクニックを用いて、1/Lという境界を1.5/Lに正確に移動させることに成功しました。一方で、人間の専門家はこの証明プロセスを確認するのに25分かかったため、AIが一部の数学的推論タスクにおいて人間を上回る処理速度を持っていることが証明されました。
さらに注目すべきは、GPT-5Proが採用した証明戦略です。凸L-スムーズ関数の二つの基本的な不等式であるBregman散度不等式と標準的な共強制性不等式を巧みに利用し、代数操作を通じて凸性条件をさらに詳細に定義し、深い数学的スキルと革新性を示しました。
人間の反撃とAIの独創性
劇的な展開が続きました。GPT-5Proの発見が注目されている間に、元の論文著者が論文のバージョンを迅速に更新し、共同研究者を追加し、1.75/Lが正確な境界値であることを証明し、以前の理論的空白を完全に埋めました。
人間の学者たちの証明アプローチも精巧で、凸L-スムーズ関数のBregman散度不等式を使用し、三つの異なるポイント対ごとに不等式を立て、それらを異なる重みで合計し、恒等式を用いて複雑な勾配項を巧妙に簡略化することで、正確な数学的境界を導き出しました。
人間の学者たちが最終的に数学的結果で勝ち取ったものの、GPT-5Proの証明アプローチは新バージョンの論文とは全く異なっていました。この違いには大きな意味があり、AIが人間の研究方向を事前に知っていたわけではないことを示しています。つまり、AIは真正の数学的推論と革新能力を持っています。
AIの数学的能力の歴史的意義
GPT-5Proの数学証明に関する突破は、深い歴史的意義を持っています。これはAIシステムが純粋な数学的推論分野で、単なる計算や知識検索の能力を越えて、真正の創造的な数学的思考の領域に入った初めての出来事です。
この能力の登場は、いくつかの分野に大きな影響を与えます。数学研究分野では、AIは数学家の強力な補助となることができ、新しい定理や証明方法の探索を支援します。工学や科学的計算分野では、AIの数学的推論能力が複雑な問題解決に新たなアプローチを提供します。教育分野では、AIは数学教育と学習の仕方を画期的に変えられるかもしれません。
さらに重要的是、この突破はAIが抽象的思考と論理的推論の潜在能力を示しています。数学的証明には厳密な論理チェーン、革新的な思考角度、深遠な洞察力が必要です。GPT-5Proがこれらの面で示した行動は、AIがより高度な知能に向かって進んでいることを示しています。
未来の無限の可能性
GPT-5Proの数学的証明能力は、AI開発における重要な節目です。モデルの能力が継続的に向上し、トレーニング方法が改善されるにつれて、AIがより多く創造的な思考を必要とする分野で突破を遂げることが期待されます。
数学定理の証明から科学的仮説の提案、工学問題の解決、芸術創作の構想に至るまで、AIの創造力は急速に拡大しています。この傾向は、私たちが人工知能の本質を理解する方法を変えるだけでなく、人間とAIとの協働のあり方も再定義することになるでしょう。
