微軟Q-Sparse模型：8B參數性能直逼7B模型 訓練微調輕鬆搞定！

在人工智能的世界裏，大型語言模型（LLMs）以其卓越的自然語言處理能力而著稱。然而，這些模型在實際應用中的部署卻面臨着巨大的挑戰，主要是因爲它們在推理階段的高計算成本和內存佔用。爲了解決這一問題，研究人員們一直在探索如何提高LLMs的效率。最近，一種名爲Q-Sparse的方法引起了廣泛關注。

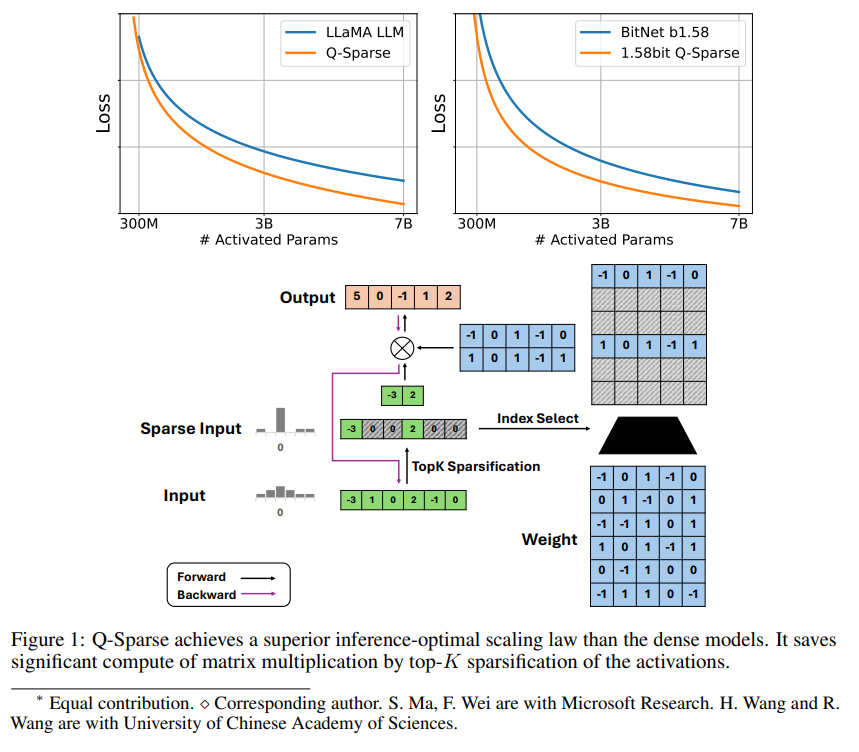
Q-Sparse是一種簡單但有效的方法，它通過在激活中應用top-K稀疏化和訓練中的直通估計器，實現了LLMs的完全稀疏激活。這意味着在推理時可以顯著提高效率。關鍵的研究成果包括:

Q-Sparse在保持與基線LLMs相當的結果的同時，推理效率更高。

提出了一種適用於稀疏激活LLMs的推理最優擴展法則。

Q-Sparse在不同設置中均有效，包括從頭開始訓練、現成LLMs的繼續訓練和微調。

Q-Sparse適用於全精度和1位LLMs（例如BitNet b1.58）。

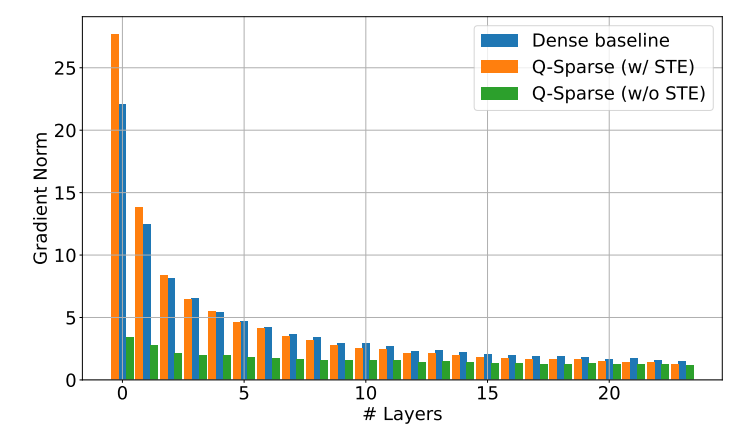
稀疏激活的優勢

稀疏性通過兩種方式提高LLMs的效率:首先，稀疏性可以減少矩陣乘法的計算量，因爲零元素不會被計算;其次，稀疏性可以減少輸入/輸出（I/O）的傳輸量，這是LLMs推理階段的主要瓶頸。

Q-Sparse通過在每個線性投影中應用top-K稀疏化函數來實現激活的全稀疏性。對於反向傳播，使用直通估計器計算激活的梯度。此外，還引入了平方ReLU函數來進一步提高激活的稀疏性。

實驗驗證

研究人員通過一系列擴展實驗研究了稀疏激活LLMs的擴展法則，並得出了一些有趣的發現:

稀疏激活模型的性能隨着模型大小和稀疏比率的增加而提高。

給定固定的稀疏比率S，稀疏激活模型的性能與模型大小N呈冪律擴展法則。

給定固定的參數N，稀疏激活模型的性能與稀疏比率S呈指數律擴展法則。

Q-Sparse不僅可以用於從頭開始訓練，還可以用於現成LLMs的繼續訓練和微調。在繼續訓練和微調設置中，研究人員使用與從頭開始訓練相同的架構和訓練過程，唯一的區別是使用預訓練權重初始化模型，並啓用稀疏函數繼續訓練。

研究人員正在探索將Q-Sparse與1位LLMs（如BitNet b1.58）和混合專家(MoE)結合使用，以進一步提高LLMs的效率。此外，他們還在努力使Q-Sparse與批量模式兼容，這將爲LLMs的訓練和推理提供更多的靈活性。